Security Constrained Optimal Power Flow

The Security Constrained Optimal Power Flow (SCOPF) problem is presented as a major challenge to be tackled by grid operators. How would you optimally operate the grid if you had to ensure the disconnection of any element does not compromise the safe operation of the system?

The complication

The best possible operating point of a network is commonly determined by an optimal power flow, ideally in its non-linear version, known as ACOPF. Even under normal conditions, solving the ACOPF is complex, involving non-linear equality constraints and a large number of inequality constraints (e.g., loading limits, voltage boundaries) that define a highly restricted search space.

The SCOPF problem extends this difficulty as it requires finding an operating point that remains feasible not only in normal operation but also under any plausible contingency. In other words, for each critical line or generator that could realistically be disconnected, the system must still operate securely. Now imagine a system with thousands of nodes: you would need to evaluate thousands of contingency scenarios to ensure that your initial setpoints make the system resilient to every possible failure. Complicated right?

The solution

At eRoots we have embedded the application of the Generalised Benders Decomposition technique (GBD). Such an approach consists of dividing the initially huge problem into:

• A master problem (MP): Determines the optimal operating point under normal conditions. As violations are discovered in the subproblems, new constraints (Benders cuts) are added to the MP to account for contingency behavior.
• A set of subproblems (SP): Each SP simulates how the system should be optimally operated following a specific contingency.

The workflow looks as follows: 

1. Solve the initial MP to determine preliminary optimal active power setpoints for the generators.
2. Evaluate all SPs to check if the MP’s active power setpoints ensure safe operation under each contingency. There is freedom to adjust the reactive power setpoints accordingly.
3. Identify violations in the SPs and feed them back into the MP in the form of linear inequalities (Benders cuts). Using our interior point solver, we can efficiently extract the necessary Lagrange multipliers and penalty terms.
4. Repeat the process until no violations are detected in any SP.

‍

Where is the bottleneck?

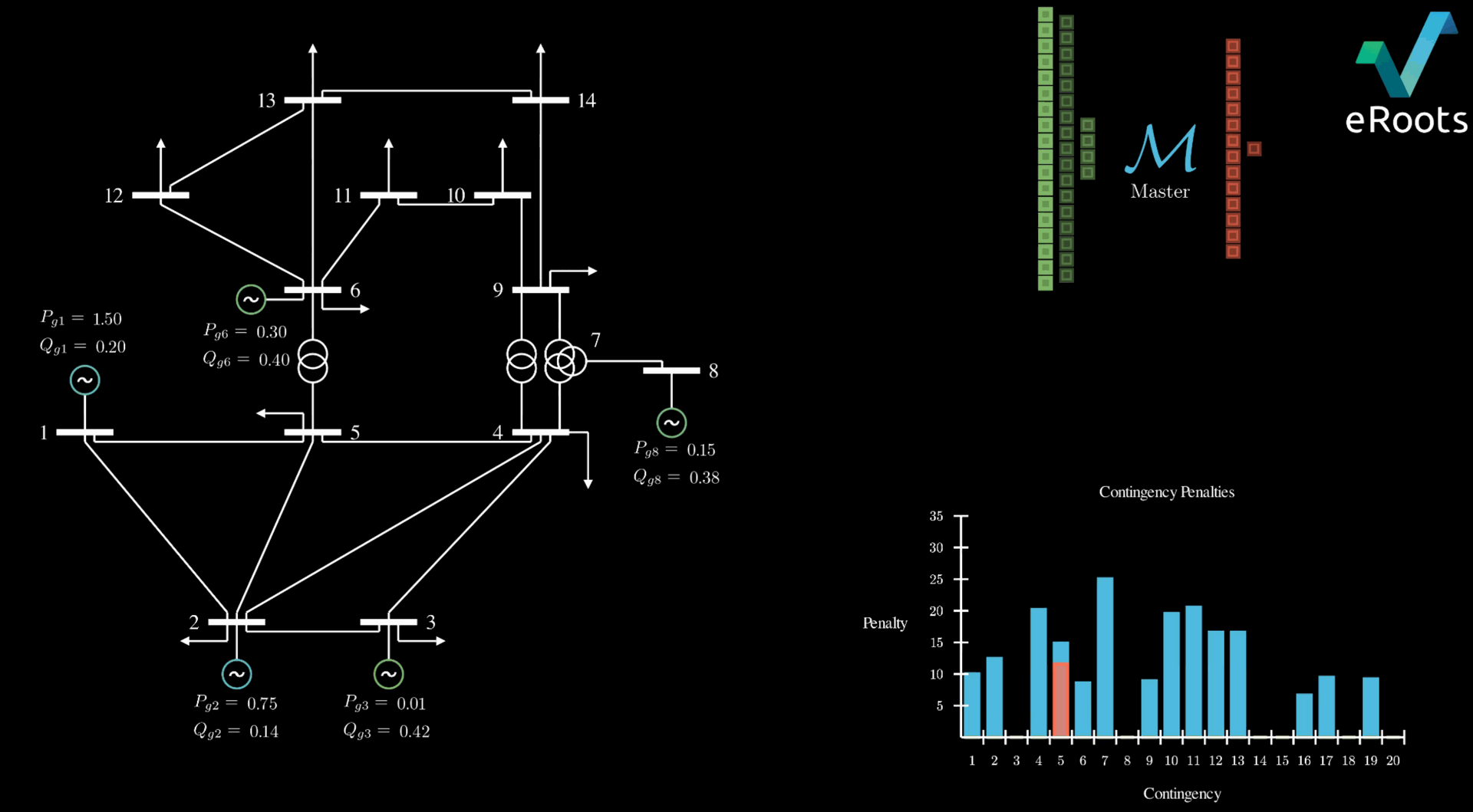
The proposed methodology allows us to decompose what otherwise would be a huge optimization problem that would consume all of a regular's computer memory and therefore become intractable. However, while GBD significantly reduces memory consumption and avoids making the SCOPF intractable, the major computational bottleneck remains: solving the SPs, which typically consumes about 99% of the total runtime.  Several strategies can mitigate this bottleneck:

• Parallelize the computation of the SPs across multiple cores. A 10x speed improvement could be expected from this.
• Rely on machine learning techniques, such as our proposed Graph Convolutional Neural Network, to predict the Lagrange multipliers and penalty costs. This would allow not having to run an ACOPF for every SP, greatly speeding up the calculation.

Stay tuned to find out how we are accelerating the solving process of such a challenging optimization problem!

‍